TEMA 2: OPERACIONES CON NÚMEROS DECIMALES:

La parte entera va a la izquierda de la coma y la parte decimal a la derecha.
Vamos a ver cada una de estas cifras decimales.
a) La décima
La décima es un valor más pequeño que la unidad
1 unidad = 10 décimas.
Es decir, si dividimos una unidad en 10 partes iguales, cada una de ellas es una décima.
Las décimas van a la derecha de la coma.
b) La centésima
Es un valor más pequeño que la unidad y también que la décima.
1 unidad = 100 centésimas
1 décima = 10 centésimas.
Es decir, si dividimos una unidad en 100 partes iguales, cada una de ellas es una centésima.
Y si dividimos una décima en 10 partes iguales, cada una de ellas es una centésima.
c) La milésima
Es un valor más pequeño que la unidad, que la décima y también que la centésima:
1 unidad = 1.000 milésimas
1 décima = 100 milésimas
1 centésima = 10 milésimas
Es decir, si dividimos una unidad en 1.000 partes iguales, cada una de ellas es una centésima.
1.- ¿Cómo se lee un número decimal?
Por ejemplo: 53,41 se puede leer de varias maneras:
"cincuenta y tres coma cuarenta y uno"
"cincuenta y tres con cuarenta y uno"
"cincuenta y tres unidades y cuarenta y una centésimas"
COMPARAR NÚMEROS DECIMALES:
Para comparar números decimales comenzamos comparando la parte entera: aquél que tenga la parte entera más alta, es el mayor.
234,65 es mayor que 136,76
Si ambos tienen igual parte entera habría que comparar la parte decimal, comenzando por las décimas, luego las centésimas y por último las milésimas.
Veamos algunos ejemplos:
146,89 es mayor que 146,78 (ambos tienen igual parte entera, pero el primero tiene 8 décimas mientras que el segundo tiene 7).
357,56 es mayor que 357,53 (ambos tienen igual parte entera y también las mismas décimas, pero el primero tiene 6 centésimas y el segundo tan sólo 3)
634,128 es mayor que 634,125 (ambos tienen igual parte entera y también las mismas décimas y centésimas, pero el primero tiene 8 milésimas y el segundo tan sólo 5)

REPRESENTAR NÚMEROS DECIMALES:
REDONDEAR NÚMEROS DECIMALES:
Para redondear un número a la unidad tenemos que fijarnos en la primera cifra después de la coma.
Si esta cifra es menor que 5 (1, 2, 3, 4) no debemos hacer nada, pero si esa cifra es 5 o mayor (5, 6, 7, 8, 9) debemos sumar una unidad al número.
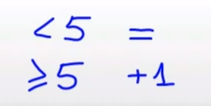
Los números decimales los podemos redondear a la unidad, a la décima o a lacentésima.
a) Redondear a la unidad
Redondear a la unidad implica sustituirlo por el número que más se le aproxime sin decimales.
Si la parte decimal es igual o inferior a 0,500 se redondea a la unidad inferior; si es mayor que 0,500 se redondea a la unidad superior.
Veamos algunos ejemplos:
43,5
Este número se sitúa entre 43 y 44. Hay que ver a cual de ellos se redondea.
La parte decimal es 0,5 (como no tiene centésimas ni milésimas equivale a 0,500). Al ser esta parte decimal igual o inferior a 0,500 redondeamos a la unidad inferior.
Por lo tanto 43,5 lo redondeamos a 43.
27,31
Este número se sitúa entre 27 y 28.
La parte decimal es 0,31 (como no tiene milésimas equivale a 0,310). Al ser esta parte decimal inferior a 0,500 redondeamos a la unidad inferior.
Por lo tanto 27,31 lo redondeamos a 27.
58,721
Este número se sitúa entre 58 y 59.
La parte decimal es 0,721. Al ser esta parte decimal superior a 0,500 redondeamos a la unidad superior.
Por lo tanto 58,721 lo redondeamos a 59.
b) Redondear a la décima
Redondear un número a la décima implica sustituirlo por el número que más se le aproxime y que en la parte decimal tan sólo tenga décimas.
Si la parte centesimal es igual o inferior a 0,050 se redondea a la décima inferior; si es mayor que 0,050 se redondea a la décima superior.
Veamos algunos ejemplos:
22,53
Este número se sitúa entre 22,5 y 22,6.
La parte centesimal es 0,03 (como no tiene milésimas equivale a 0,030). Al ser esta parte centesimal inferior a 0,050 redondeamos a la décima inferior.
Por lo tanto 22,53 lo redondeamos a 22,5.
62,27
Este número se sitúa entre 62,2 y 62,3.
La parte centesimal es 0,07 (como no tiene milésimas equivale a 0,070). Al ser esta parte centesimal superior a 0,050 redondeamos a la décima superior.
Por lo tanto 62,27 lo redondeamos a 62,3.
84,662
Este número se sitúa entre 84,6 y 84,7.
La parte centesimal es 0,062. Al ser esta parte centesimal superior a 0,050 redondeamos a la décima superior.
Por lo tanto 84,662 lo redondeamos a 84,7.
c) Redondear a la centésima
Redondear un número a la centésima implica sustituirlo por el número que más se le aproxime y que en la parte decimal tenga hasta centésimas.
Si la parte milesimal es igual o inferior a 0,005 se redondea a la centésima inferior; si es mayor que 0,005 se redondea a la centésima superior.
Veamos algunos ejemplos:
17,124
Este número se sitúa entre 17,12 y 17,13.
La parte milesimal es 0,004. Al ser esta parte milesimal inferior a 0,005 redondeamos a la centésima inferior.
Por lo tanto 17,124 lo redondeamos a 17,12.
26,33
Este número se sitúa entre 26,33 y 26,34.
La parte milesimal es 0,000. Al ser esta parte milesimal inferior a 0,005 redondeamos a la centésima inferior.
Por lo tanto 26,33 lo redondeamos a 26,33.
77,258
Este número se sitúa entre 77,25 y 77,26.
La parte milesimal es 0,008. Al ser esta parte milesimal superior a 0,005 redondeamos a la centésima superior.
Por lo tanto 77,258 lo redondeamos a 77,26.
Redondear a la décima el siguiente número: 10, 386
Separando el número por las décimas quedaría 10,3 — 86. Nos fijamos en el número siguiente a las décimas y es el 8. Como es mayor que 5 tendremos que sumar 1 a la última cifra del número:
10,3 –> 10,4

SUMAR Y RESTAR NÚMEROS DECIMALES:
La suma y resta con números decimales es exactamente igual que con números enteros. Lo único que hay que vigilar es que cada tipo de cifra vaya en su columna:
Las centenas en la columna de centenas, las decenas en la de decenas, las unidades en la de unidades, las décimas en la de décimas, las centésimas en la de centésimas...
Vamos a ver un ejemplo:
Un fallo que se suele cometer al operar con números decimales es alinear todos los números a la derecha:


MULTIPLICAR NÚMEROS DECIMALES:
En una multiplicación pude haber decimales en cualquiera de los dos factores, o en los dos:

a) En primer lugar multiplicamos sin tener en cuenta que hay decimales:

b) A continuación contamos los números decimales que hay en ambos factores y serán las cifras decimales que lleve el resultado:
b.1.- Empecemos por la primera multiplicación,

Tiene una cifra decimal en el primer factor y ninguna en el segundo: en total 1 cifra decimal.
El resultado de la multiplicación (324.324) llevará 1 cifra decimal:

- Multiplicar por 10, 100, 1.000
Por ejemplo:
45,6 x 10
235,6 x 100
78,96 x 1.000
Para calcular el resultado:
a) Primero escribimos en el resultado el primer factor.
b) Luego en el resultado desplazaremos la coma a la derecha tantas posiciones como ceros lleve el número por el que hemos multiplicado.
Puede ocurrir que haya más ceros que cifras decimales, por lo que no podamos desplazar a la derecha la coma tantas posiciones como ceros.
¿Qué hacemos? Las posiciones que no hayamos podido desplazar la coma la completaremos con ceros:
Veamos los ejemplos:
a) 45,6 x 10
Primeros repetimos en el resultado el primer factor.
45,6 x 10 = 45,6
Luego desplazaremos la coma a la derecha una posición ya que hemos multiplicado por 10 que lleva 1 cero:
45,6 x 10 = 456, (la coma a la derecha sin ninguna cifra decimal se puede quitar y escribir 456)
b) 235,6 x 100
Primeros repetimos en el resultado el primer factor.
235,6 x 100 = 235,6
Luego desplazaremos la coma a la derecha dos posiciones ya que hemos multiplicado por 100 que lleva 2 ceros:
Como 235,6 tan sólo tiene un decimal y necesitamos desplazar la coma 2 posiciones, completaremos el movimento que nos falta poniendo 1 cero:
235,6 x 100 = 23.560
c) 78,96 x 1.000
Primeros repetimos en el resultado el primer factor.
78,96 x 1.000 = 78,96
Luego desplazaremos la coma a la derecha tres posiciones ya que hemos multiplicado por 1.000 que lleva 3 ceros.
Como 78,96 tan sólo tiene dos decimales y necesitamos desplazar la coma 3 posiciones, completaremos el movimento que nos falta poniendo 1 cero:
78,96 x 1.000 = 78.960
1.- LOS MÚLTIPLOS DE UN NÚMERO
Para calcular los múltiplos de un nº debemos multiplicar ese número por cualquier otro.
Ejemplo: 7, 14, 21, 28, 35, 42, ... son múltiplos de 7 (porque todos ellos, resultan de multiplicar 7 por la sucesión de números naturales).
“Ten en cuenta”: Para comprobar si un número es múltiplo de otro, debemos hacer una división y que ésta sea exacta.
Ejemplo: Un número (a) es múltiplo de otro (b), si la división de a:b es exacta.
Ej: 40 (a) es múltiplo de 5 (b) porque 40: 5 = 8 y el resto es cero.
NOTA: (Si la división no es Exacta, ambos números no son múltiplos).
Ejemplo:
14 : 3 = 4, y en el resto queda 2. Por tanto, 14 no es múltiplo de 3.
- Múltiplos de un número (I)
- Múltiplos de un número (II)
- Múltiplos de un número (III)
- Múltiplos de un número (IV)
- Múltiplos de un número (V)
2.- MÍNIMO COMÚN MÚLTIPLO (m.c.m.)
- El mínimo común múltiplo (m.c.m.) de dos o más números es el menor de losmúltiplos comunes (distinto de cero) de dichos números.
- Ejemplo: Calcula el m.c.m. de 2 y 3
* Múltiplos de 2 : 0, 2, 4, 6, 8, 10, 12, 14, 16, 18, 20, 22, 24, ...
* Múltiplos de 3: 0, 3, 6, 9, 12, 15, 18, 21, 24, 27, 30, ...
El número común más pequeño (distinto de cero) es el 6
Por tanto, el m.c.m. (2 y 3) = 6
- Otro ejemplo: Calcula el m.c.m. de (3, 4 y 6)
* Múltiplos de 3: 0, 3, 6, 9, 12, 15, 18, 21, 24, 27, 30, 33, 36, ...
* Múltiplos de 4: 0, 4, 8, 12, 16, 20, 24, 28, 32, 36, 40, ...
* Múltiplos de 6: 0, 6, 12, 18, 24, 30, 36, 42, 48, ...
El número común más pequeño (distinto de cero) es el 12.
Por tanto, el m.c.m. de (3, 4 y 6) = 12
- Mínimo Común Múltiplo de dos números
- Mínimo Común Múltiplo 2
- Mínimo Común Múltiplo 3
3.- DIVISORES DE UN NÚMERO
* Un número (b) es divisor de otro (a), si la división a ÷ b es exacta.
* Si (b) es divisor de (a), entonces (a) es múltiplo de (b).
Ejemplo: a = 21 (a) : (b)
b = 3 21 : 3 = 7 (21) es múltiplo de (3)
(3) es divisor de (21)
* NOTA: Para calcular todos los divisores de un número, lo dividimos entre los número naturales menores que él, y anotamos los que den división exacta, es decir, resto cero.
“TEN EN CUENTA”:- Los números que tienen sólo dos divisores se llaman PRIMOS.
Ej: 2, 3, 5, 7, ....
- Los números que tienen más de dos divisores se llaman COMPUESTOS.
Ej: 4, 6, 8, 9, 10, ...
- Enlace 1
- Enlace 2
- Enlace 3 (Jclic: Cuando enlaces, pica en "ejecutar")
- Enlace 4
- Enlace 5
- Enlace 6
- Enlace 7
4.- LOS CRITERIOS DE DIVISIBILIDAD
* Los criterios de divisibilidad nos permiten descubrir si un número es divisible por otro sin necesidad de hacer la división.
POR 2: Un nº es divisible por 2 si es par (es decir, si acaba en 0, 2, 4, 6 u 8).
POR 3: Un nº es divisible por 3 si la suma de todas sus cifras es múltiplo de 3.
POR 5: Un nº es divisible por 5 si termina en 0 ó en 5.
POR 9: Un nº es divisible por 9 si la suma de todas sus cifras es múltiplo de 9.
POR 10: Un nº es divisible por 10 si termina en 0.
5.- MÁXIMO COMÚN DIVISOR (m.c.d.)
* El Máximo Común Divisor (m.c.d.) de dos o más números, es el mayor de todos los divisores comunes de dichos números.
* Para calcular el m.c.d. De dos números, sigue los siguientes pasos:
1º) Calcula todos los divisores de cada número (Recuerda: De cada división exacta obtendrás dos divisores de ese nº) .
2º) Busca los divisores comunes de ambos números.
3º) El mayor de esos divisores comunes será el m.c.d.
Ejemplo: Calcula el m.c.d. de (12 y 16):
1º) Calcula los divisores de cada nº:
Divisores de 12, son: 1, 2, 3, 4, 6 y 12.Divisores de 16, son: 1, 2, 4, 8 y 16.
2º) Busca los divisores comunes: 1, 2 y 4.
3º) El mayor de esos divisores comunes es el 4.
Por tanto el m.c.d. de (12 y 16) es 4
- Máximo Común divisor
- Máximo Común Divisor 3
TEMA 3: DIVIDIR NÚMEROS DECIMALES
DIVISIÓN DE UN NÚMERO DECIMAL POR UNO ENTERO:
Se hace la división como si fueran nº naturales, pero se pone una coma en el cociente al bajar la primera cifra decimal.
LA PROPIEDAD DE LA DIVISIÓN:
Si se multiplica el Dividendo y el Divisor por un mismo nº; se obtiene el mismo cociente.
Ej: 12 : 4 = 3 ……. 12 x 5 = 60 …………. 60 : 20 = 3
4 x 5 = 20
- División de un Nº decimal entre un Nº entero (I)
- División de un Nº decimal entre un Nº entero (II)
- División de un Nº decimal entre un Nº entero (III)
- Jclic: División de un decimal entre un entero
DIVISIÓN POR LA UNIDAD SEGUIDA DE CEROS:
Para dividir números decimales por la unidad seguida de ceros (10, 100, 1000...) se desplaza la coma a la izquierda tantos lugares como ceros lleve detrás la unidad, y si fuera necesario se colocan ceros (para rellenar los huecos vacíos).
Ejemplo: 29,7 : 10= 2,97
297 : 100= 2,97
- División de un Nº por la Unidad seguida de ceros (I)
- División de un Nº por la Unidad seguida de ceros (II)
DIVISIÓN DE DOS NÚMEROS DECIMALES:
1º) Se transforma el divisor en un nº entero, y para conseguir esto, debemos multiplicar el dividendo y el divisor por la unidad seguida de tantos ceros como cifras decimales tenga el divisor.
2º) Se realiza la división con normalidad.
NOTA: Para obtener varios decimales en el cociente, se ponen ceros en el dividendo.
- División de un Nº decimal entre otro Nº decimal (I)
- División de un Nº decimal entre otro Nº decimal (II)
- División entre nº decimales
- Jclic: División entre dos nº decimales
TEMA 4: MÚLTIPLOS Y DIVISORES:
1.- LOS MÚLTIPLOS DE UN NÚMEROTEMA 4: MÚLTIPLOS Y DIVISORES:
Para calcular los múltiplos de un nº debemos multiplicar ese número por cualquier otro.
Ejemplo: 7, 14, 21, 28, 35, 42, ... son múltiplos de 7 (porque todos ellos, resultan de multiplicar 7 por la sucesión de números naturales).
“Ten en cuenta”: Para comprobar si un número es múltiplo de otro, debemos hacer una división y que ésta sea exacta.
Ejemplo: Un número (a) es múltiplo de otro (b), si la división de a:b es exacta.
Ej: 40 (a) es múltiplo de 5 (b) porque 40: 5 = 8 y el resto es cero.
NOTA: (Si la división no es Exacta, ambos números no son múltiplos).
Ejemplo:
14 : 3 = 4, y en el resto queda 2. Por tanto, 14 no es múltiplo de 3.
- Múltiplos de un número (I)
- Múltiplos de un número (II)
- Múltiplos de un número (III)
- Múltiplos de un número (IV)
- Múltiplos de un número (V)
2.- MÍNIMO COMÚN MÚLTIPLO (m.c.m.)
- El mínimo común múltiplo (m.c.m.) de dos o más números es el menor de losmúltiplos comunes (distinto de cero) de dichos números.
- Ejemplo: Calcula el m.c.m. de 2 y 3
* Múltiplos de 2 : 0, 2, 4, 6, 8, 10, 12, 14, 16, 18, 20, 22, 24, ...
* Múltiplos de 3: 0, 3, 6, 9, 12, 15, 18, 21, 24, 27, 30, ...
El número común más pequeño (distinto de cero) es el 6
Por tanto, el m.c.m. (2 y 3) = 6
- Otro ejemplo: Calcula el m.c.m. de (3, 4 y 6)
* Múltiplos de 3: 0, 3, 6, 9, 12, 15, 18, 21, 24, 27, 30, 33, 36, ...
* Múltiplos de 4: 0, 4, 8, 12, 16, 20, 24, 28, 32, 36, 40, ...
* Múltiplos de 6: 0, 6, 12, 18, 24, 30, 36, 42, 48, ...
El número común más pequeño (distinto de cero) es el 12.
Por tanto, el m.c.m. de (3, 4 y 6) = 12
- Mínimo Común Múltiplo de dos números
- Mínimo Común Múltiplo 2
- Mínimo Común Múltiplo 3
3.- DIVISORES DE UN NÚMERO
* Un número (b) es divisor de otro (a), si la división a ÷ b es exacta.
* Si (b) es divisor de (a), entonces (a) es múltiplo de (b).
Ejemplo: a = 21 (a) : (b)
b = 3 21 : 3 = 7 (21) es múltiplo de (3)
(3) es divisor de (21)
* NOTA: Para calcular todos los divisores de un número, lo dividimos entre los número naturales menores que él, y anotamos los que den división exacta, es decir, resto cero.
“TEN EN CUENTA”:- Los números que tienen sólo dos divisores se llaman PRIMOS.
Ej: 2, 3, 5, 7, ....
- Los números que tienen más de dos divisores se llaman COMPUESTOS.
Ej: 4, 6, 8, 9, 10, ...
- Enlace 1
- Enlace 2
- Enlace 3 (Jclic: Cuando enlaces, pica en "ejecutar")
- Enlace 4
- Enlace 5
- Enlace 6
- Enlace 7
4.- LOS CRITERIOS DE DIVISIBILIDAD
* Los criterios de divisibilidad nos permiten descubrir si un número es divisible por otro sin necesidad de hacer la división.
POR 2: Un nº es divisible por 2 si es par (es decir, si acaba en 0, 2, 4, 6 u 8).
POR 3: Un nº es divisible por 3 si la suma de todas sus cifras es múltiplo de 3.
POR 5: Un nº es divisible por 5 si termina en 0 ó en 5.
POR 9: Un nº es divisible por 9 si la suma de todas sus cifras es múltiplo de 9.
POR 10: Un nº es divisible por 10 si termina en 0.
5.- MÁXIMO COMÚN DIVISOR (m.c.d.)
* El Máximo Común Divisor (m.c.d.) de dos o más números, es el mayor de todos los divisores comunes de dichos números.
* Para calcular el m.c.d. De dos números, sigue los siguientes pasos:
1º) Calcula todos los divisores de cada número (Recuerda: De cada división exacta obtendrás dos divisores de ese nº) .
2º) Busca los divisores comunes de ambos números.
3º) El mayor de esos divisores comunes será el m.c.d.
Ejemplo: Calcula el m.c.d. de (12 y 16):
1º) Calcula los divisores de cada nº:
Divisores de 12, son: 1, 2, 3, 4, 6 y 12.Divisores de 16, son: 1, 2, 4, 8 y 16.
2º) Busca los divisores comunes: 1, 2 y 4.
3º) El mayor de esos divisores comunes es el 4.
Por tanto el m.c.d. de (12 y 16) es 4
- Máximo Común divisor
- Máximo Común Divisor 3
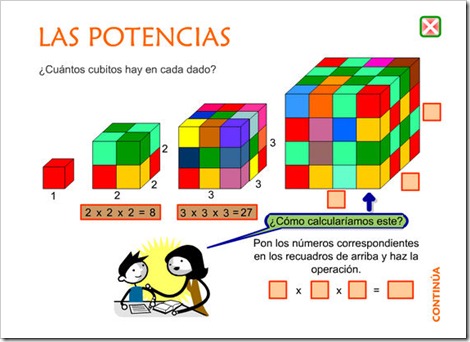
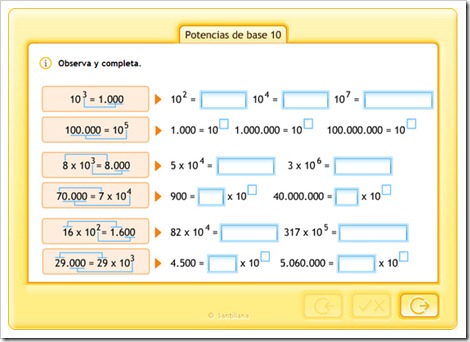
TEMA 5: POTENCIAS Y RAÍCES
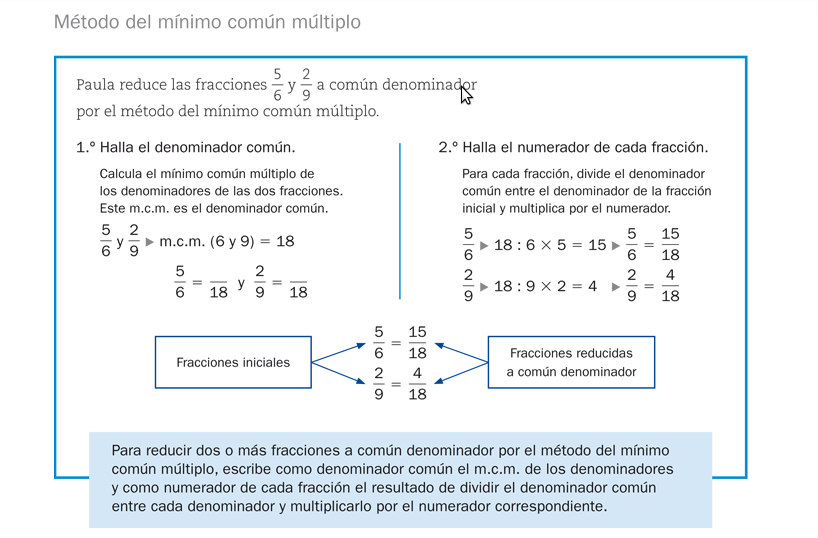
TEMA 6: LAS FRACCIONES
¿Cómo se leen las fracciones? Se leen en función de cuál es su denominador:
1 / 2: un medio
1 / 3: un tercio
1 / 4: un cuarto
1 / 5: un quinto
1 / 6: un sexto
1 / 7: un séptimo
1 / 8: un octavo
1 / 9: un noveno
1 / 10: un décimo
1 / 11: un onceavo
1 / 12: un doceavo
1 / 13: un treceavo